20 min read

PC: Nature-Magazine-Robot-Hands

This article contains heuristics for following:

  • Parallel jaw grasps.
  • Suction grasps.
  • Linear push policies for improving parallel jaw grasps.
  • Toppling policies for improving suction grasps.

Grasping is one of the fundamental subtask of a robotic manipulation pipeline. Both learning based and physics / geometry based grasping methods can benefit from grasp sampling heuristics in this article. Even if you are using a large arm farm to teach your robots the skills of grasping, you can save your robots quite a lot of time with these heuristics. This article summarizes the most common grasp sampling heuristics used in literature.

Some of the common ways to use these heuristics are:

  • Generating labels for learning based grasp planners (offline): 6-DOF GraspNet [4] uses these samplers for evaluation with physics based simulation. Grasps that retain the object between the gripper are considered successful after a predefined shaking motion. DexNet [2][3] evaluates these grasps based on analytic quasi-static grasp wrench space (GWS) analysis. Both methods score these sampled grasps based on how good they are in resisting disturbances. These scores are used as labels for training the grasp planners.
  • During grasp synthesis (inference): DexNet [2][3] uses these sampled grasps as seeds for Cross Entropy Method (CEM), and optimizes grasps based on predicted grasp quality from GQ-CNN (Grasp Quality Convolutional Network). Traditional geometric methods, prune these candidate grasps if they are kinematically infeasible or if they result in collision between gripper and other objects or environment. The best of these samples are picked for execution.

We will summarize the details of heuristics for each type of grippers used for manipulation.

Parallel jaw grasps

Parallel jaw grasps jam the object between the grippers (Most often the grippers have rubber on them to increase the size of friction cones and thus the robustness of the grasp). Typically, the success of parallel jaw grasp depends on local geometry around the grasp point like if the grasp fits inside the gripper, friction btw gripper and object surface, mass of the object.

Force Closure: If the contact points on the object are such that forces applied on those points don’t result in slippage and can resist gravity then force closure ( object doesn’t move with respect to the gripper ) is achieved, the grasp is considered successful.

Parametrization: Parallel Jaw Grasps are typically parametrized by 6-DOF pose of the gripper with initial configuration of open gripper.

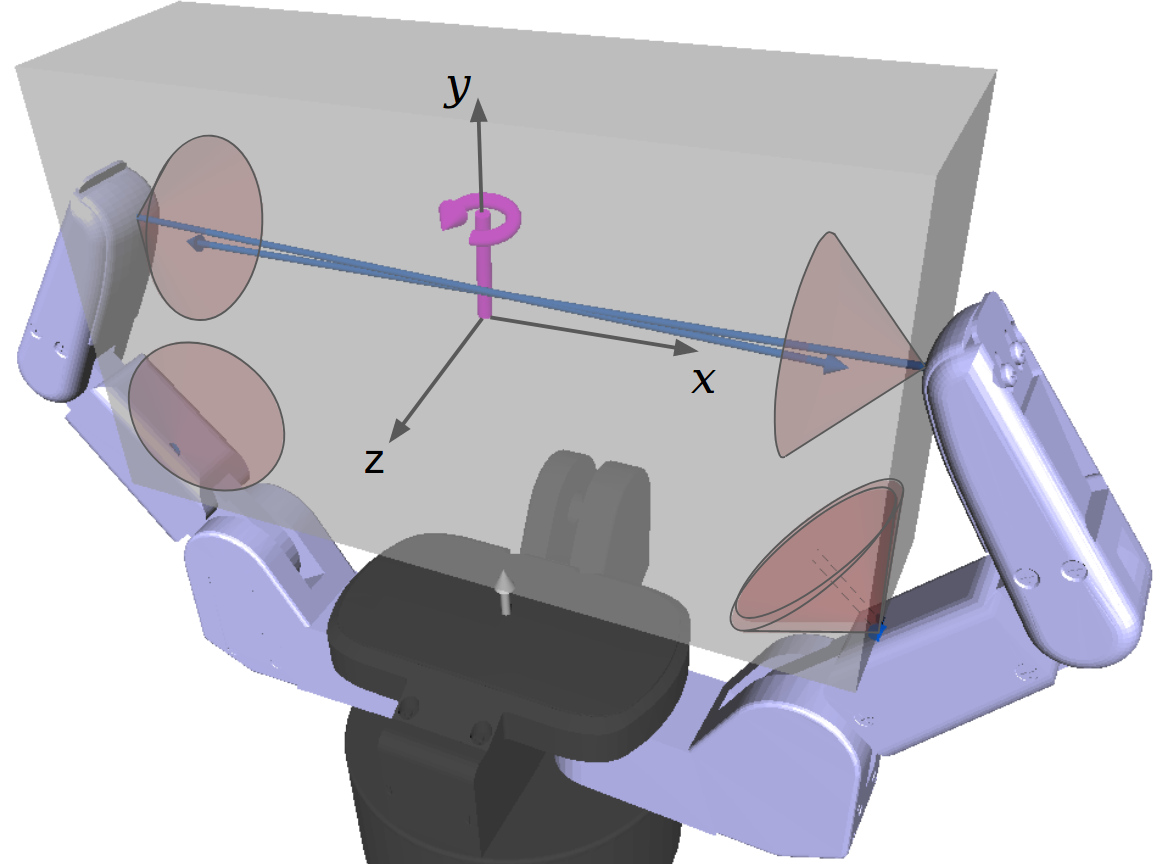
Illustration shows the friction cones and forces applied by fingers at contact points on a cuboid. This illustration doesn’t account for gravity. Picture Credit: https://arxiv.org/abs/1905.00134v2

A Billion ways to grasp [1] summarizes several heuristics for parallel jaw grippers and evaluates their precision and coverage w.r.t a uniform sampler.

Assumption: Access to the 3D triangle mesh or 3D point cloud of the object so that surface normals can be computed.

Here are the two most effective heuristics that are purely based on geometry:

Approach based samplers:

These methods are characterized by approach vector of the gripper (red-dashed line) which typically aligns with normal to the palm (purple axis).

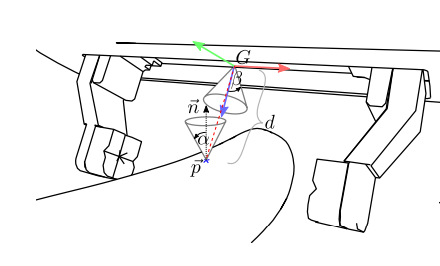
Approach based sampler. Picture Credit: Billion ways to Grasp [1]

Pseudo code for approach based sampler:

Notations:

  • G β†’ Gripper frame.
  • \(purple, red, green\) β†’ \(z, y, x\) of the gripper frame G.
  • \(\vec{p}\) β†’ Randomly chosen point on object surface.
  • \(\vec{n}\) β†’ Surface normal at point \(\vec{p}\).
  • \(d\) β†’ distance from gripper origin \(\vec{g}\) to point \(\vec{p}\)
  • \(\vec{gp}\) β†’ Gripper approach direction.
  • Ξ± β†’ angle between \(\vec{n}\) and \(\vec{gp}\)
  • Ξ² β†’ angle between z axis of gripper frame G and gripper approach \(\vec{gp}\)

For generating each sample:

  • Sample normal vector \(\vec{p}\) from the surface of the object.
  • Ξ± β†’ uniform_sample(0, Ο€/2)
  • Ξ² β†’ 0
  • d β†’ uniform_sample(0, L)
  • Ξ³ β†’ uniform_sample(0, 2Ο€)
  • Choose the gripper sample pose \(\hat{G}\) such that sampled Ξ±, Ξ², Ξ³ and d satisfied.
  • If sample \(\hat{G}\) results in collision with the object or object volume between the fingers is zero, discard the sample.

Antipodal based samplers:

These methods sample directly on the space of possible contact points and try to exploit the grasps that create force closure.

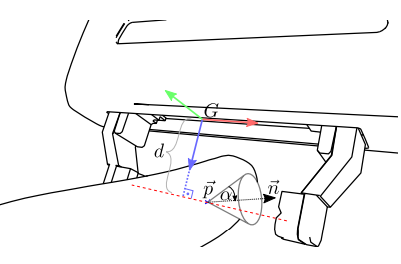
Antipodal based sampler. Picture Credit: Billion ways to Grasp [1]

Pseudo code for antipodal grasp sampler:

Notations:

  • G β†’ Gripper frame.
  • \({purple, red, green}\) β†’ \({z, y, x}\) of the gripper frame G.
  • \(\vec{p}\) β†’ Randomly chosen point on object surface.
  • \(\vec{n}\) β†’ Surface normal at point \(\vec{p}\).
  • \(s_{min}\) β†’ distance from gripper origin \(\vec{g}\) to closest on antipodal grasp ray (Stand-off distance)
  • \(\alpha\) β†’ Angle between the normal \(\vec{n}\) and antipodal grasp ray.
  • \(\gamma\) β†’ rotation around antipodal grasp ray.

For generating each sample

  • sample a point \(\vec{p}\) on the object surface
  • \(\alpha\) β†’ uniform_sample(0, \(\pi/6\))
  • \(s_{min}\) β†’ 0
  • \(\gamma\) β†’ uniform_sample(0, \(2\pi\))
  • Antipodal point \(p^{\prime}\) is choosen such that farthest intersection point along the antipodal grasp ray.
  • Choose grasp sample \(\hat{G}\) with the center of line segment \(\vec{p}\) \(\vec{p}^\prime\) + \(d\) and rotatated \(\gamma\) w.r.t antipodal grasp ray. If sample \(\hat{G}\) results in collision with the object or object volume between the fingers is zero, discard the sample.

Comparing the two parallel-jaw heuristics

Billion ways to grasp [1] evaluates grasps based on two metrics:

  • Robust coverage: Percent of robust grasps (still successful in a small Ο΅-neighborhood) sampled w.r.t oracle uniform sampler. This is very similar to recall.
  • Precision: Percent of the successful grasps among the sampled.

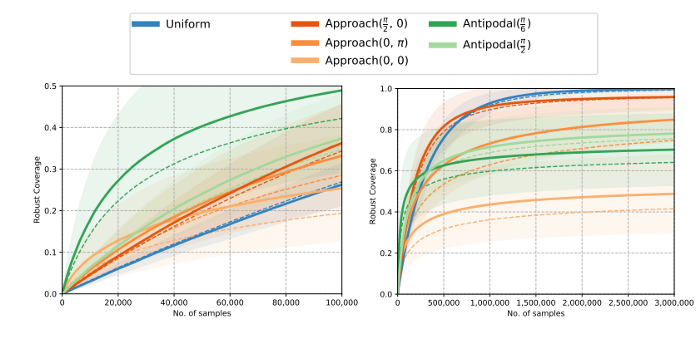
Robust coverage vs number of grasp samples. We only look at Uniform, Approach(Ο€/2, 0) and Antipodal(Ο€/6), which are best in each category. (Higher is better)

Precision of each category. Approach(Ο€/2, 0) and Antipodal(Ο€/6), which are best in each category. Higher is better during inference.

As seen by the conclusion of Billion ways to grasp[1] from the tables, if you have a limited sampling budget antipodal sampling scheme provides both highest coverage and precision. However, asymptotically misses several ground truth grasps. These correspond to small scale features on objects and along the edges of objects.

Visual illustration of what these sampled successful grasps and robust successful grasps look like. Each point is the grasp center and notice how robust grasps are clustered around object parts that fit nicely inside the gripper.

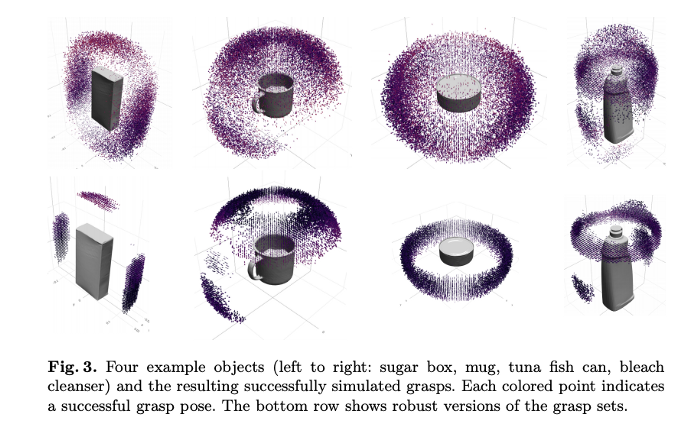
Picture Credit: Billion ways to Grasp [1]

Suction grippers

Suction grippers form vacuum seal on the surface of the object and if that vacuum force is sufficient to resist the gravity and external wrenches, the grasp is robust. Typically suction grasp success depends on surface porousness, local geometry, mass and payload capacity of the suction gripper. These grippers are most popular for pick and place of objects in warehouse order fulfillment. DexNet 4.0 [6] which is one of the best published bin-picking system that uses composite policy between suction and parallel jaw grasps, chooses suction grasps for about 82% of attempts.

Parametrization: Suction grasps are typically parameterized by point p on the object surface and approach vector v as illustrated below.

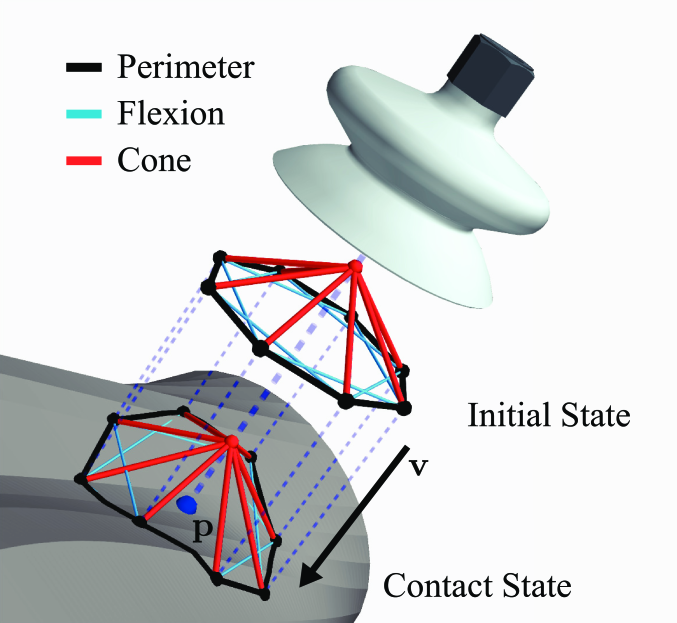
Illustration of seal formation on non-planar surface from DexNet 3.0 [3]

Planarity Centroid Heuristic:

Since successful suction grasps prefer planar non-porous surfaces, these heuristics try to find sufficiently planar surfaces on the object that are closer to COM (Center of Mass). Approach vectors are chosen along the surface normal because large motion tangential to surface might result in vacuum seal breakage.

Pseudo code for planarity centroid heuristic:

Notations:

  • \(\vec{p}\) β†’ Suction point on the surface of the object.
  • \(\vec{v}\) β†’ Approach vector for suction grasp.
  • \(COM\) β†’ Center of Mass
  • \(PC_{full}\) β†’ Full point cloud of the scene.
  • \(PC_{exclude}\) β†’ Exclude point cloud. \(PC_{0} = \emptyset\) for the \(1^{st}\) sample.

For generating each sample:

  • Fit a plane to point cloud data \(PC_{full}\) using RANSAC excluding \(PC_{exclude}\).
  • Sample a planar patch of vaccum cup size on the plane closest to COM.
  • \(\vec{p_i}\) β†’ Center of the planar patch.
  • \(\vec{v_i}\) β†’ -ve of the normal at that point.
  • Add inliers of the sampled patch to \(PC_{exclude}\)
  • Choose the suction grasp \(G_i={p_i, v_i}\) that is closest to COM

Some examples of successful suction grasps on 3D meshes are visualized below.

Illustrates suction grasps on diverse objects from DexNet 3.0 [3]dataset. Each point is a suction grasp sample with red β†’ failed grasp and green β†’ successful grasp.

DexNet 3.0 [3] evaluates suction grasps in physical robot trials based on two metrics:

  • Average Precision: Area under the precision / recall curve. How good is the heuristic in scoring high quality grasps ?
  • Success Rate: Fraction of the grasps that were successful.

Object categories used for physical robot experiments in DexNet 3.0 [3]

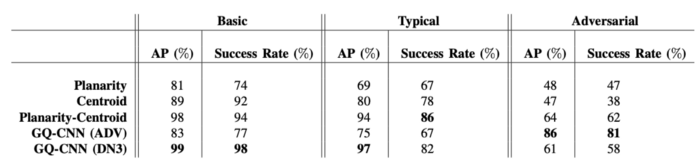
How well each heuristic performed on different objects in robot physical experiments. Picture credit: DexNet 3.0 [3]. For both metrics higher is better.

As can be seen from the table above, Planarity Centroid Heuristic does quite well compared to even learnt method DexNet 3.0 [3] on basic and typical objects.

Some of the failure cases of suction grasps are categorized as below:

Failure cases from DexNet 3.0 [3]. Imperceptible objects have small holes in them or have high curvature that prevents the vacuum seal and Impossible objects are porous.

Adaptive sampler:

These methods use heuristics that exploit the geometry to generate seed samples (described above) and further optimize the grasp according to grasp quality metric. Most often these are blackbox optimization technique such as cross entropy method (CEM) that doesn’t exploit object geometry. Although CEM is an optimization algorithm used in many areas, I would still consider it a heuristic since it doesn’t exploit the object geometries while sampling.

Additional assumption: Access to grasp quality function such as DexNet 2.0 / DexNet 3.0 Grasp Quality Network (GQ-CNN) or ability to evaluate quality of grasps in realtime based on GWS.

Cross Entropy Method (CEM)

Notations:

  • m β†’ Number of iterations
  • n β†’ Number of intital grasp samples.(These are 6-DOF gripper pose \(\hat{G}\) for parallel jaw and \({\vec{p}, \vec{v}}\) for suction grasp).
  • \(U\) β†’ Set of grasp samples.
  • \(\xi\) β†’ Set of elite samples.
  • \(\gamma\) β†’ Elite percentage, subset of the initial samples from \(U\). Typically < 50%
  • \(k\) β†’ Number of mixtures used in gaussian mixture model (GMM) \(M\).
  • \(Q_{\theta}\) β†’ Grasp Quality Function.

Algorithm:

\(U\) β†’ Uniform sample of grasps \(\hat{G}_i\). For i = 1, … m:

  • \(\xi\) β†’ top \(\gamma\) percentile of \(U\) ranked by \(Q_{\theta}\)
  • \(M\) β†’ Fit GMM to \(\xi\) with \(k\) mixtures.
  • \(U\) β†’ n iid samples from \(M\).

Return the best grasp according to \(\arg\max_{u \in U} Q_{\theta}\)

If you were familiar with CEM, you may have noticed the use of GMM instead of Gaussians and this is because distribution of grasps on most objects are multi-modal.

Some examples of applying CEM method to DexNet 2.0 (parallel jaw grasps )and DexNet 3.0 (suction grasps) grasp quality functions to generate most robust grasps.

CEM method used by DexNet 2.0 [2] Marked in Black is the grasp output by CEM, which is very close to global maximum according to the robustness predictions \(𝑄_πœƒ\)

CEM method used by DexNet 3.0 [3] Also, in this case CEM method finds the best suction grasp predicted by π‘„πœƒ

Improving chances of grasping

Sometimes neither suction grasp not parallel jaw grasp is able to pick up any object in the heap. This is mostly due to inability to perceive robust grasps (occlusion) or inability to execute the perceived grasp ( collision or kinematic infeasibility ). In those cases non-prehensile ( fancy word for non-graspable ) actions are executed to either singulate the object to expose enough clearance for parallel jaw grasps or topple the object to expose a planar surface for suction grasps.

CAUTION: The following policies have not been tested on a real robot, so the results and conclusions don’t necessarily transfer.

Parametrization: Push vector (p, q) where p = {x, y, z} starting point and q = {x’, y’, z’} is the end point.

Linear Pushing

Linear pushing policies typically help with separating the object heap so that parallel jaw grasps are accessible.

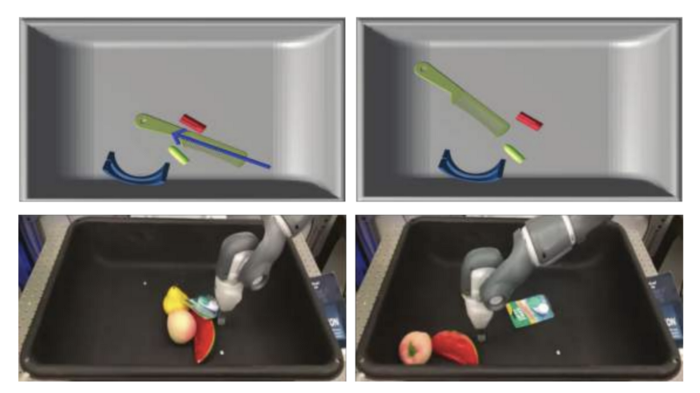
Illustration of linear pushing before (left) and after (right) in simulation (above) and real robot (below). PC: [5]

Additional assumptions: Semantic instance segmentation of the objects on the bin so that each objects position on the bin is observed. Free space segmentation of the bin is also used in the linear pushing policies for choosing the push direction.

Free Space Policy:

Aims to separate the two closest objects in the heap by pushing them towards the free space.

Pseudo-code:

Notations:

  • \(\hat{c_i}\) & \(\hat{c_j}\) β†’ Center of mass estimates of two closest objects in the heap.
  • \(p_i\) & \(p_j\) β†’ Maximal free space points that are closest to \(\hat{c_i}\) & \(\hat{c_j}\) respectively.

Algorithm:

  • Find 2 closest objects with COM \(\hat{c_i}\) & \(\hat{c_j}\)
  • Draw lines \(\overline{c_ip_i}\) & \(\overline{c_jp_j}\) to the corresponding maximal free space points.
  • For each object \(i\) find collision free (between gripper & other objects / bin) push segment that goes through COM \(c_i\) and closest to \(\overline{c_ip_i}\).
  • Choose the push segment \(\overline{cp}\) with the shortest length.

Boundary Shear Policy:

Aims to separate two closest objects in the heap by pushing one of the objects along the boundary between the objects.

Pseudo-code:

Notations:

  • \(\hat{c_i}\) & \(\hat{c_j}\) β†’ Center of mass estimates of two closest objects in the heap.

Algorithm:

  • Find 2 closest objects with COM \(\hat{c_i}\) & \(\hat{c_j}\)
  • Construct the line \(\overline{c_ic_j}\) projected to the support surface and it’s perpendicular \(\overline{c_ic_j}_{\bot}\)
  • Generate 4 possible push vectors parallel to \(\overline{c_ic_j}_{\bot}\) and passing through \(\hat{c_i}\) & \(\hat{c_j}\) in each direction.
  • Choose the push direction closest to free space and collision freel.

Facilitating Grasping [5] evaluates above policies and few others in simulation in clearing the object heaps that don’t have accessible grasps and measures the confidence gain of both grasp types. As can be seen the linear pushing policies make the parallel jaw grasps more accessible than suction grasps.

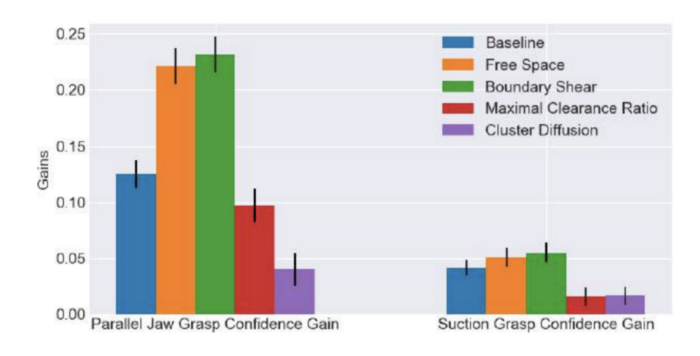
Confidence gain of both parallel jaw and suction grasping policy on according Facilitating Grasping [5]

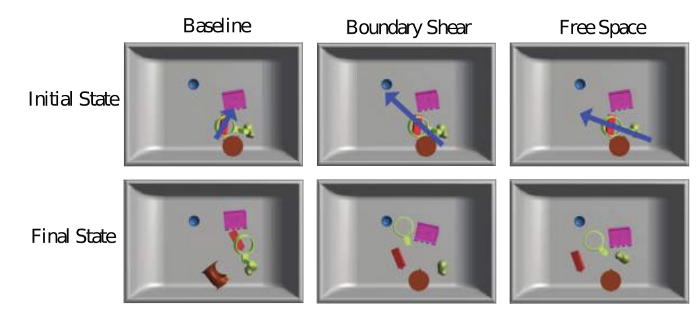
Example of before / after of linear pushing policies described above in simulated object heaps. PC: Facilitating Grasping [5].

Singulated Object Toppling

Facilitating grasping [5] also explores policies for toppling a singulated known 3D object so that quality of suction grasp after toppling can be improved.

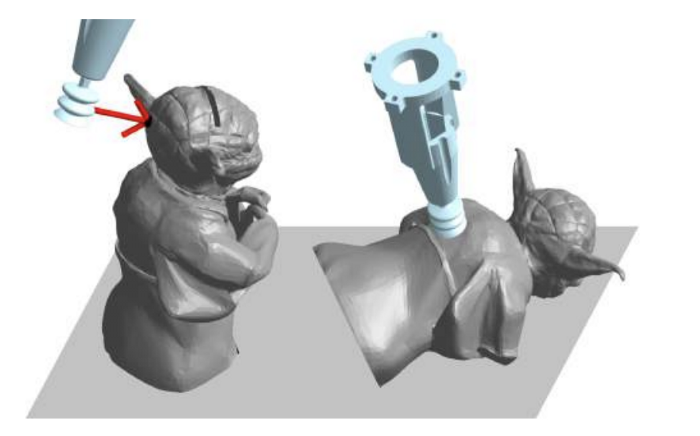
Topping to facilitate the top-down suction grasp. PC: Facilitating grasping [5]

Assumptions: Known 3D object with known transition distribution of stable resting poses \(P(x_{t+1} / x_t, u_t)\) and access to suction grasp quality function \( V_s(x_t) \).

Max Height Policy:

Highest possible point on the object that has surface normal within 15 degree of the supporting plane normal. This policy only gets executed if \(V_s(x_{t+1}) > V_s(x_t)\).

Greedy Policy:

Pick the action that makes the expected suction grasp more accessible.

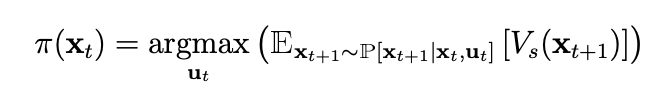
Facilitating grasping [5] evaluates these policies in simulation and compares against a policy that runs complete value iteration based on \(P(x_{t+1} / x_t, u_t)\) and \(V_s(x_t)\).

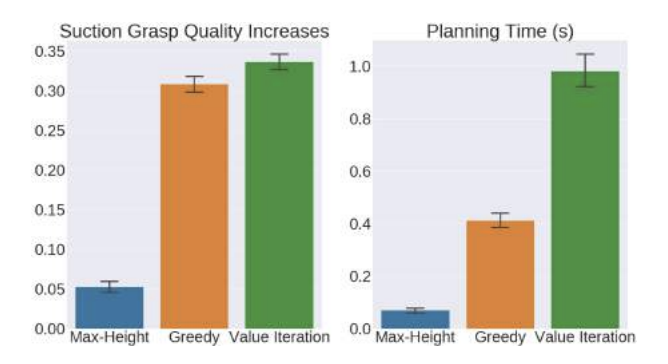
The greedy toppling policy does fairly well compared to best performing value iteration with much less runtime PC: [5]

Conclusion:

This post explored different subtasks used for grasping and several effective heuristics for them. Please explore the references for more details on learning based / more effective policies. These heuristics are meant to provide intuition on each of the grasping subtasks and how they measure up to some of the more advanced methods.

References:

[1] A Billion Ways to Grasp: An Evaluation of Grasp Sampling Schemes on a Dense, Physics-based Grasp Data Set

[2] Dex-Net 2.0: Deep Learning to Plan Robust Grasps with Synthetic Point Clouds and Analytic Grasp Metrics

[3] Dex-Net 3.0: Computing Robust Robot Vacuum Suction Grasp Targets in Point Clouds using a New Analytic Model and Deep Learning

[4] 6-DOF GraspNet: Variational Grasp Generation for Object Manipulation

[5] Facilitating Robotic Grasping using Pushing and Toppling

[6] Dex-Net 4.0: Learning ambidextrous robot grasping policies